Σκοπός του Μαθήματος :

Οι σπουδαστές να είναι σε θέση να κατανοούν το πώς λειτουργεί ο ανατοκισμός, η προεξόφληση, ποιες είναι οι εφαρμογές των ραντών. Να είναι σε θέση να αξιολογούν επενδύσεις, υπολογίζοντας την Καθαρή Παρούσα Αξία και την Εσωτερική Απόδοση Επένδυσης. Να κατανοούν τα οριακά οικονομικά μεγέθη, να μπορούν να υπολογίζουν αποσβέσεις και τα πλεονάσματα παραγωγού και καταναλωτή.

Στόχοι του μαθήματος :

Με την ολοκλήρωση του μαθήματος ο σπουδαστής είναι σε θέση να:

• Να γνωρίζει πώς λειτουργεί ο ανατοκισμός, η προεξόφληση, ποιες είναι οι εφαρμογές των ραντών.
• Να κατανοεί  τα συνολικά, μέσα και οριακά οικονομικά μεγέθη
• Να αξιολογεί επενδύσεις
• Να υπολογίζει τις αποσβέσεις, την καθαρή παρούσα αξία, την ΙRR, το πλεόνασμα του παραγωγού και καταναλωτή

Παλιά Θέματα Εξετάσεων

Παρακάτω παραθέτουμε τα Παλιά Θέματα Εξετάσεων του μαθήματος Μαθηματικά των Επιχειρήσεων του Σεπτεμβρίου 2012.

Παλιά Θέματα Εξετάσεων_Σεπτέμβριος 2013_Λύσεις

Παρακάτω παραθέτουμε το Τυπολόγιο για τις Ασκήσεις των Χρηματοοικονομικών:

Τυπολόγιο_Χρηματοοικονομικα

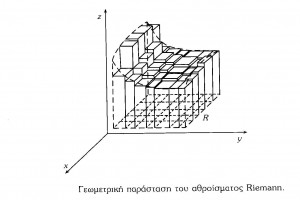
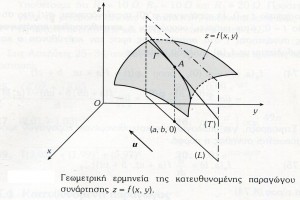
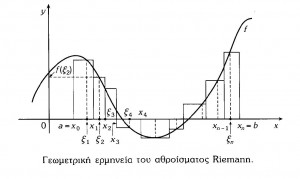
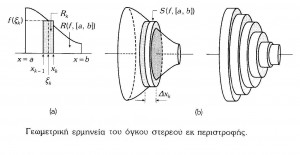
ΕΝΙΑΙΟ ΛΥΚΕΙΟ

Αλλαγές πραγματοποιούνται τα επόμενα χρόνια, από το Υπουργείο Παιδείας, για την Εισαγωγή των υποψηφίων στην Τριτοβάθμια Εκπαίδευση. Έτσι, με το νέο καθεστώς δίνεται βάρος στα μαθήματα γενικής παιδείας στις δύο πρώτες τάξεις του λυκείου και μειώνονται τα μαθήματα που θα εξετάζονται στις Πανελλήνιες.

Α΄ Λυκείου

Η Α’ Λυκείου παραμένει τάξη γενικής παιδείας και περιλαμβάνει πρόγραμμα 35 διδακτικών ωρών την εβδομάδα. Από τις οποίες οι 33 ώρες καλύπτουν τα παρακάτω εννέα μαθήματα κοινά για όλους :

1) Γλώσσα

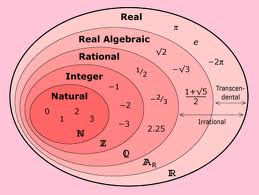
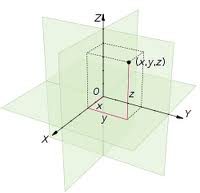
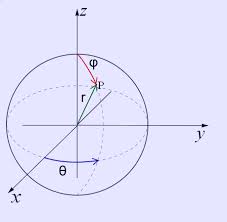
2) Μαθηματικά

3) Φυσικές επιστήμες

4) Θρησκευτικά

5) Ιστορία

6) Ξένη Γλώσσα

7) Φυσική Αγωγή

8) Πολιτική Παιδεία

9) Ερευνητική Εργασία

Ενώ οι υπόλοιπες δύο ώρες θα περιλαμβάνουν τα παρακάτω μαθήματα επιλογής :

I) Εφαρμογές Πληροφορικής ή

II) Τεχνολογία και Διαχείριση Φυσικών Πόρων ή

III) Έκφραση – Πολιτισμός Read more »

Μαθηματικά ΙΙΙ

Περιγραφή Μαθήματος

1. Διανυσματικός Λογισμός του R³ (Συστήματα καρτεσιανών συντεταγμένων στο χώρο, Διανύσματα στο R³, Εσωτερικό Γινόμενο και Εφαρμογές, Εξωτερικό Γινόμενο και Εφαρμογές.)
2. Γραμμική Άλγεβρα του χώρου Rⁿ (Ευκλείδειος χώρος Rⁿ, Πίνακες, Ορίζουσες, Γραμμικοί μετασχηματισμοί, Τετραγωνικές μορφές.)
3. Συναρτήσεις μεταξύ Ευκλείδειων χώρων (Πραγματικές συναρτήσεις πολλών μεταβλητών, Γραφική παράσταση συναρτήσεων πολλών μεταβλητών, Διανυσματικές συναρτήσεις πολλών μεταβλητών.)
4. Η Τοπολογία του Rⁿ (Μπάλες και ορθογώνια του Rⁿ, Ακολουθίες του Rⁿ, Εσωτερικά σημεία, Συνοριακά σημεία και σημεία συσσώρευσης, Ανοικτά και κλειστά σύνολα του Rⁿ, Συμπαγή σύνολα, Συνεκτικά σημεία.)
5. Σύγκλιση και Συνέχεια Διανυσματικών Συναρτήσεων (Όρια πραγματικών και διανυσματικών συναρτήσεων, Συνεχείς διανυσματικές συναρτήσεις, Ομοιόμορφη συνέχεια διανυσματικών συναρτήσεων.)
6. Διαφορίσιμες Πραγματικές Συναρτήσεις Πολλών Μεταβλητών (Μερική παράγωγος, Διαφορικό, Γραμμική προσέγγιση(γραμμικοποίηση) συνάρτησης, κατευθυνόμενη παράγωγος.)
7. Διαφορίσιμες Διανυσματικές Συναρτήσεις Πολλών Μεταβλητών (Παραγωγίσιμες παραμετρήσεις, Ολοκληρώσιμες παραμετρήσεις, Παράγωγος και διαφορικό διανυσματικών συναρτήσεων, Κανόνας αλυσίδας, Μέγιστα και ελάχιστα.)
8. Διπλό Ολοκλήρωμα (Διπλό ολοκλήρωμα σε ορθογώνιο και γενικό χωρίο, Αλλαγή μεταβλητής διπλού ολοκληρώματος, Εφαρμογές διπλού ολοκληρώματος.)
9. Τριπλό Ολοκλήρωμα (Τριπλό ολοκλήρωμα σε ορθογώνιο και γενικό χωρίο, Τεχνικές υπολογισμού τριπλών ολοκληρωμάτων, Αλλαγή μεταβλητής τριπλού ολοκληρώματος, Εφαρμογές τριπλού ολοκληρώματος.)
10. Επικαμπύλιο Ολοκλήρωμα (Παραμετρήσεις και παραμετρικές καμπύλες του R³, Μήκος παραμετρικής καμπύλης, Αριθμητικό επικαμπύλιο ολοκλήρωμα, Διανυσματικό επικαμπύλιο ολοκλήρωμα.)

Μαθηματικά ΙΙ

Περιγραφή Μαθήματος

1. Πραγματικοί Αριθμοί (Αξιώματα του Συνόλου R των πραγματικών αριθμών, Το επεκταμένο σύνολο των πραγματικών αριθμών, Οι Φυσικοί αριθμοί, Τέλεια επαγωγή. )
2. Ακολουθίες Πραγματικών Αριθμών (Όρια ακολουθιών, Μονότονες ακολουθίες, Υποακολουθίες, Ακολουθίες Cauchy, Ειδικά κριτήρια σύγκλισης ακολουθιών, Ανώτερο και κατώτερο όριο ακολουθίας.)
3. Σειρές Πραγματικών Αριθμών και Δυναμοσειρές (Σύγκλιση σειρών πραγματικών αριθμών, Απόλυτη σύγκλιση σειρών, Τα σταθερά κριτήρια σύγκλισης σειρών, Αναδιατάξεις και γινόμενα σειρών, Σύγκλιση Δυναμοσειρών.)
4. Πραγματικές Συναρτήσεις (Η έννοια της πραγματικής συνάρτησης, Πράξεις και διάταξη, Ταξινόμηση πραγματικών συναρτήσεων, Τριγωνομετρικές και κυκλομετρικές συναρτήσεις, Εκθετικές και λογαριθμικές συναρτήσεις, Οι υπερβολικές συναρτήσεις. )
5. Σύγκλιση Συναρτήσεων (Σημεία συσσώρευσης συνόλου, Όρια συναρτήσεων, Επεκτάσεις της έννοιας του ορίου.)
6. Συνεχείς Συναρτήσεις (Έννοια της συνέχειας, Τα θεμελιώδη θεωρήματα των συνεχών συναρτήσεων, Ομοιόμορφη συνέχεια. )
7. Παραγωγίσιμες Συναρτήσεις (Εφαπτομένη ευθεία και ρυθμοί μεταβολής, Παράγωγος συνάρτησης, Κανόνες παραγώγισης, Παράγωγοι υπερβατικών συναρτήσεων, Διαφορικό και γραμμικές προσεγγίσεις, Τα κύρια θεωρήματα του διαφορικού λογισμού.)
8. Εφαρμογές της Παραγώγου (Πεπλεγμένη παραγώγιση, Μέγιστα και ελάχιστα, Κυρτότητα και σημεία καμπής, Ασύμπτωτες, Γραφική παράσταση, Μέθοδος Newton, Παράγωγος παραμετρήσεων, Επίπεδη κίνηση. )
9. Αόριστο Ολοκλήρωμα (Έννοια του αορίστου ολοκληρώματος, Γενικές μέθοδοι αόριστης ολοκλήρωσης, Ολοκλήρωση ρητών συναρτήσεων, Ολοκλήρωση ειδικών συναρτήσεων, Εφαρμογές του αόριστου ολοκληρώματος. )
10. Ορισμένο Ολοκλήρωμα (Riemann) (Το πρόβλημα του Εμβαδού, Η έννοια του ορισμένου ολοκληρώματος, Ιδιότητες του Ορισμένου ολοκληρώματος, Τα θεμελιώδη θεωρήματα του Απειροστικού λογισμού, Αριθμητική ολοκλήρωση.)

Μαθηματικά Ι

Περιγραφή Μαθήματος

1. Φυσικοί, Ακέραιοι, Ρητοί Αριθμοί
2. Η Πληρότητα των Πραγματικών Αριθμών
3. Ακολουθίες Πραγματικών Αριθμών
4. Όρια Συναρτήσεων
5. Σειρές
6. Συνεχείς Συναρτήσεις
7. Ομοιόμορφη Συνέχεια
8. Θεώρημα Ενδιάμεσης Τιμής
9. Το Ολοκλήρωμα Riemann
10. Η Ολοκληρωσιμότητα των Συνεχών Συναρτήσεων
11. Χαρακτηρισμός Ολοκληρωσίμων Συναρτήσεων
12. Στοιχεία Διαφορικού Λογισμού

Παρέχονται Σημειώσεις και Λυμένα Θέματα Εξετάσεων για την καλύτερη κατανόηση του μαθήματος, καθώς και για την βέβαιη επιτυχία. Πραγματοποιούμε Ιδιαίτερα Μαθηματικών με μεγάλη εμπειρία και εξειδίκευση.

Απειροστικός Λογισμός ΙΙΙ

Περιγραφή Μαθήματος

1. Σύνολα και Συναρτήσεις
2. Διανυσματικός Λογισμός του R³ (Συστήματα καρτεσιανών συντεταγμένων στο χώρο, Διανύσματα στο R³, Εσωτερικό Γινόμενο και Εφαρμογές, Εξωτερικό Γινόμενο και Εφαρμογές.)
3. Αναλυτική Γεωμετρία του χώρου R³ (Παραμετρήσεις και παραμετρικές καμπύλες του R³, Η ευθεία του χώρου R³, Επιφάνειες και εξισώσεις, Επίπεδο του χώρου R³ , Η σφαίρα, Κυλινδρικές επιφάνειες και επιφάνειες εκ περιστροφής, Τετραγωνικές Επιφάνειες, Κυλινδρικές και σφαιρικές συντεταγμένες.)
4. Γραμμική Άλγεβρα του χώρου Rⁿ (Ευκλείδειος χώρος Rⁿ, Πίνακες, Ορίζουσες, Γραμμικοί μετασχηματισμοί, Τετραγωνικές μορφές.)
5. Συναρτήσεις μεταξύ Ευκλείδειων χώρων (Πραγματικές συναρτήσεις πολλών μεταβλητών, Γραφική παράσταση συναρτήσεων πολλών μεταβλητών, Διανυσματικές συναρτήσεις πολλών μεταβλητών.)
6. Η Τοπολογία του Rⁿ (Μπάλες και ορθογώνια του Rⁿ, Ακολουθίες του Rⁿ, Εσωτερικά σημεία, Συνοριακά σημεία και σημεία συσσώρευσης, Ανοικτά και κλειστά σύνολα του Rⁿ, Συμπαγή σύνολα, Συνεκτικά σημεία.)
7. Σύγκλιση και Συνέχεια Διανυσματικών Συναρτήσεων (Όρια πραγματικών και διανυσματικών συναρτήσεων, Συνεχείς διανυσματικές συναρτήσεις, Ομοιόμορφη συνέχεια διανυσματικών συναρτήσεων.)
8. Διαφορίσιμες Πραγματικές Συναρτήσεις Πολλών Μεταβλητών (Μερική παράγωγος, Διαφορικό, Γραμμική προσέγγιση(γραμμικοποίηση) συνάρτησης, κατευθυνόμενη παράγωγος.)
9. Διαφορίσιμες Διανυσματικές Συναρτήσεις Πολλών Μεταβλητών (Παραγωγίσιμες παραμετρήσεις, Ολοκληρώσιμες παραμετρήσεις, Παράγωγος και διαφορικό διανυσματικών συναρτήσεων, Κανόνας αλυσίδας, Μέγιστα και ελάχιστα.) Read more »

Απειροστικός Λογισμός ΙΙ

Περιγραφή Μαθήματος

1. Σύνολα και Συναρτήσεις
2. Πραγματικοί Αριθμοί (Αξιώματα του Συνόλου R των πραγματικών αριθμών, Το επεκταμένο σύνολο των πραγματικών αριθμών, Οι Φυσικοί αριθμοί, Τέλεια επαγωγή. )
3. Ακολουθίες Πραγματικών Αριθμών (Όρια ακολουθιών, Μονότονες ακολουθίες, Υποακολουθίες, Ακολουθίες Cauchy, Ειδικά κριτήρια σύγκλισης ακολουθιών, Ανώτερο και κατώτερο όριο ακολουθίας.)
4. Σειρές Πραγματικών Αριθμών και Δυναμοσειρές (Σύγκλιση σειρών πραγματικών αριθμών, Απόλυτη σύγκλιση σειρών, Τα σταθερά κριτήρια σύγκλισης σειρών, Αναδιατάξεις και γινόμενα σειρών, Σύγκλιση Δυναμοσειρών.)
5. Διανυσματικός Λογισμός του R² (Συστήματα καρτεσιανών συντεταγμένων στο επίπεδο, Διανύσματα στο R², Εσωτερικό Γινόμενο και Εφαρμογές.)
6. Πραγματικές Συναρτήσεις (Η έννοια της πραγματικής συνάρτησης, Πράξεις και διάταξη, Ταξινόμηση πραγματικών συναρτήσεων, Τριγωνομετρικές και κυκλομετρικές συναρτήσεις, Εκθετικές και λογαριθμικές συναρτήσεις, Οι υπερβολικές συναρτήσεις. )
7. Σύνοψη της Αναλυτικές Γεωμετρίας του R² (Καμπύλες και εξισώσεις του R², Η ευθεία του R², Αλλαγή αξόνων καρτεσιανών συντεταγμένων, Κωνικές τομές, Η γενική εξίσωση δευτέρου βαθμού, Παραμετρήσεις και παραμετρικές καμπύλες του R², Πολικές συντεταγμένες και Πολικές εξισώσεις.)
8. Σύγκλιση Συναρτήσεων (Σημεία συσσώρευσης συνόλου, Όρια συναρτήσεων, Επεκτάσεις της έννοιας του ορίου.)
9. Συνεχείς Συναρτήσεις (Έννοια της συνέχειας, Τα θεμελιώδη θεωρήματα των συνεχών συναρτήσεων, Ομοιόμορφη συνέχεια. )
10. Παραγωγίσιμες Συναρτήσεις (Εφαπτομένη ευθεία και ρυθμοί μεταβολής, Παράγωγος συνάρτησης, Κανόνες παραγώγισης, Παράγωγοι υπερβατικών συναρτήσεων, Διαφορικό και γραμμικές προσεγγίσεις, Τα κύρια θεωρήματα του διαφορικού λογισμού.) Read more »

Απειροστικός Λογισμός Ι

Περιγραφή Μαθήματος

1. Αλγεβρικές Ιδιότητες Πραγματικών Αριθμών
2. Φυσικοί, Ακέραιοι, Ρητοί Αριθμοί
3. Η Πληρότητα των Πραγματικών Αριθμών
4. Ακολουθίες Πραγματικών Αριθμών
5. Το Θεώρημα Bolzano – Weierstrass
6. Σειρές
7. Συναρτήσεις
8. Συνεχείς Συναρτήσεις
9. Ομοιόμορφη Συνέχεια
10. Θεώρημα Ενδιάμεσης Τιμής
11. Οι απαρχές του Ολοκληρωτικού Λογισμού
12. Το Ολοκλήρωμα Riemann
13. Η Ολοκληρωσιμότητα των Συνεχών Συναρτήσεων
14. Χαρακτηρισμός Ολοκληρωσίμων Συναρτήσεων
15. Ολοκλήρωμα Riemann – Stieltjes
16. Όρια Συναρτήσεων
17. Στοιχεία Διαφορικού Λογισμού (Το πρώτο Θεμελιώδες Θεώρημα του Απειροστικού Λογισμού)

Παρέχονται Σημειώσεις και Λυμένα Θέματα Εξετάσεων για την καλύτερη κατανόηση του μαθήματος, καθώς και για την βέβαιη επιτυχία. Πραγματοποιούμε Πανεπιστημιακά Φροντιστήρια Μαθηματικών με μεγάλη εμπειρία και εξειδίκευση.