Μαθηματικά ΙΙ
Περιγραφή Μαθήματος
- Πραγματικοί Αριθμοί (Αξιώματα του Συνόλου R των πραγματικών αριθμών, Το επεκταμένο σύνολο των πραγματικών αριθμών, Οι Φυσικοί αριθμοί, Τέλεια επαγωγή. )
- Ακολουθίες Πραγματικών Αριθμών (Όρια ακολουθιών, Μονότονες ακολουθίες, Υποακολουθίες, Ακολουθίες Cauchy, Ειδικά κριτήρια σύγκλισης ακολουθιών, Ανώτερο και κατώτερο όριο ακολουθίας.)
- Σειρές Πραγματικών Αριθμών και Δυναμοσειρές (Σύγκλιση σειρών πραγματικών αριθμών, Απόλυτη σύγκλιση σειρών, Τα σταθερά κριτήρια σύγκλισης σειρών, Αναδιατάξεις και γινόμενα σειρών, Σύγκλιση Δυναμοσειρών.)
- Πραγματικές Συναρτήσεις (Η έννοια της πραγματικής συνάρτησης, Πράξεις και διάταξη, Ταξινόμηση πραγματικών συναρτήσεων, Τριγωνομετρικές και κυκλομετρικές συναρτήσεις, Εκθετικές και λογαριθμικές συναρτήσεις, Οι υπερβολικές συναρτήσεις. )
- Σύγκλιση Συναρτήσεων (Σημεία συσσώρευσης συνόλου, Όρια συναρτήσεων, Επεκτάσεις της έννοιας του ορίου.)
- Συνεχείς Συναρτήσεις (Έννοια της συνέχειας, Τα θεμελιώδη θεωρήματα των συνεχών συναρτήσεων, Ομοιόμορφη συνέχεια. )
- Παραγωγίσιμες Συναρτήσεις (Εφαπτομένη ευθεία και ρυθμοί μεταβολής, Παράγωγος συνάρτησης, Κανόνες παραγώγισης, Παράγωγοι υπερβατικών συναρτήσεων, Διαφορικό και γραμμικές προσεγγίσεις, Τα κύρια θεωρήματα του διαφορικού λογισμού.)

- Εφαρμογές της Παραγώγου (Πεπλεγμένη παραγώγιση, Μέγιστα και ελάχιστα, Κυρτότητα και σημεία καμπής, Ασύμπτωτες, Γραφική παράσταση, Μέθοδος Newton, Παράγωγος παραμετρήσεων, Επίπεδη κίνηση. )
- Αόριστο Ολοκλήρωμα (Έννοια του αορίστου ολοκληρώματος, Γενικές μέθοδοι αόριστης ολοκλήρωσης, Ολοκλήρωση ρητών συναρτήσεων, Ολοκλήρωση ειδικών συναρτήσεων, Εφαρμογές του αόριστου ολοκληρώματος. )
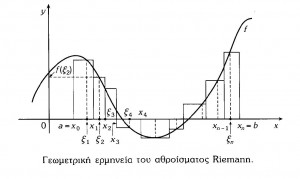
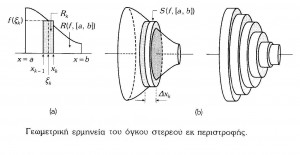
- Ορισμένο Ολοκλήρωμα (Riemann) (Το πρόβλημα του Εμβαδού, Η έννοια του ορισμένου ολοκληρώματος, Ιδιότητες του Ορισμένου ολοκληρώματος, Τα θεμελιώδη θεωρήματα του Απειροστικού λογισμού, Αριθμητική ολοκλήρωση.)

 August 1st, 2013
August 1st, 2013