Απειροστικός Λογισμός ΙΙΙ

Περιγραφή Μαθήματος

1. Σύνολα και Συναρτήσεις
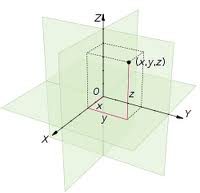
2. Διανυσματικός Λογισμός του R³ (Συστήματα καρτεσιανών συντεταγμένων στο χώρο, Διανύσματα στο R³, Εσωτερικό Γινόμενο και Εφαρμογές, Εξωτερικό Γινόμενο και Εφαρμογές.)
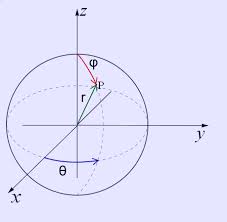
3. Αναλυτική Γεωμετρία του χώρου R³ (Παραμετρήσεις και παραμετρικές καμπύλες του R³, Η ευθεία του χώρου R³, Επιφάνειες και εξισώσεις, Επίπεδο του χώρου R³ , Η σφαίρα, Κυλινδρικές επιφάνειες και επιφάνειες εκ περιστροφής, Τετραγωνικές Επιφάνειες, Κυλινδρικές και σφαιρικές συντεταγμένες.)
4. Γραμμική Άλγεβρα του χώρου Rⁿ (Ευκλείδειος χώρος Rⁿ, Πίνακες, Ορίζουσες, Γραμμικοί μετασχηματισμοί, Τετραγωνικές μορφές.)
5. Συναρτήσεις μεταξύ Ευκλείδειων χώρων (Πραγματικές συναρτήσεις πολλών μεταβλητών, Γραφική παράσταση συναρτήσεων πολλών μεταβλητών, Διανυσματικές συναρτήσεις πολλών μεταβλητών.)
6. Η Τοπολογία του Rⁿ (Μπάλες και ορθογώνια του Rⁿ, Ακολουθίες του Rⁿ, Εσωτερικά σημεία, Συνοριακά σημεία και σημεία συσσώρευσης, Ανοικτά και κλειστά σύνολα του Rⁿ, Συμπαγή σύνολα, Συνεκτικά σημεία.)
7. Σύγκλιση και Συνέχεια Διανυσματικών Συναρτήσεων (Όρια πραγματικών και διανυσματικών συναρτήσεων, Συνεχείς διανυσματικές συναρτήσεις, Ομοιόμορφη συνέχεια διανυσματικών συναρτήσεων.)
8. Διαφορίσιμες Πραγματικές Συναρτήσεις Πολλών Μεταβλητών (Μερική παράγωγος, Διαφορικό, Γραμμική προσέγγιση(γραμμικοποίηση) συνάρτησης, κατευθυνόμενη παράγωγος.)
9. Διαφορίσιμες Διανυσματικές Συναρτήσεις Πολλών Μεταβλητών (Παραγωγίσιμες παραμετρήσεις, Ολοκληρώσιμες παραμετρήσεις, Παράγωγος και διαφορικό διανυσματικών συναρτήσεων, Κανόνας αλυσίδας, Μέγιστα και ελάχιστα.) Read more »